[논문 리뷰] RepQ-ViT: Reparameterization for Post-Training Quantization of Vision Transformers

1. Introduction

ViT를 통해 Self-attention mechanism을 이용하는 Transformer가 Vision 분야에 도입된 이후, classification, object detection, semantic segmentation 등 다양한 vision 분야에서 Transformer의 잠재력과 우수성을 확인할 수 있었습니다. 하지만 이런 ViT는 model의 크기가 크고 계산량이 많기 때문에(특히, attention 계산 과정에서) resource가 제한된 엣지 디바이스(클라우드 서버가 아닌 데이터 소스의 물리적 위치나 그 근처에서 컴퓨팅일 수행하는 장치)에서 그대로 사용하기엔 한계가 있습니다.

 

이러한 문제를 해결하기 위해선 ViT를 적절히 Quantization 하는 것이 중요합니다.

Quantization 방법에는 크게 PTQ(Post-training quantization)와 QAT(Quantization-aware training)가 있습니다. QAT는  quantization을 위해 training dataset 전체를 이용해 pre-trained된 model을 end-to-end retraining하는 방법입니다. 반대로 PTQ는 quantization parameter를 calibaration하기 위해 dataset의 일부(calibration dataset)만 이용할 수 있으며 retraining을 필요로 하지 않습니다.  QAT가 PTQ에 비해 우수한 성능을 보이나, 전체 dataset에 접근이 가능해야하고 end-to-end retrainig과정을 거쳐야 한다는 점에서 ViT를 resource-constrained edge devices 사용하기에는 PTQ가 더 적절하다고 할 수 있습니다.

 

ViT quantization 이전에 많은 PTQ 방법들이 CNN(Convolutional Neural Network)의 quantization을 위해 제안되었으나 이 방법들을 ViT에 적용시켰을 때는 성능이 좋지 못하였습니다. ViT에서 중요한 역할을 하는 LayerNorm, Softmax, GELU의 사용이 기존 CNN의 PTQ 방법을 사용할 경우의 performance 감소에 큰 영향을 미치기 때문에 이러한 부분에 초점을 맞춰 다양한 ViT quantization 방법이 제시되기도 했습니다. 하지만 여전히 성능을 불만족스러웠고 저자는 이를 이러한 방법들이 기존의 전통적인 quantization paradigm을 따르기 때문이라고 하였습니다. 여기서 전통적인 quantizaiton paradigm이란 target hardward의 특성을 고려하여 여기에 맞게 quantizatier를 design하는 것이라고 보시면 됩니다. 

 

이러한 traditional quantization-inference dependency paradigm을 해결하기 위해서 저자는 quantization과 inference과정의 분리를 시도합니다.

 

구체적으로,  위의 그림에서 볼 수 있듯이, 초기 quantization 과정에선 original parameter의 distribution을 잘 유지하기 위해 complex quantizer를 사용하고 실제 inference 과정에선 reparameterization을 통해 simple hardware-friendly quantizers로 변환시키는 방법을 사용하였습니다. 이를 바탕으로 저자는 ViT를 위한 새로운 framework인 RepQ-ViT를 제안합니다. 이 framework는 ViT에서  post-LayerNorm activations와 post-Softmax activations 두 component의 quantization에 집중합니다. 

 

2. Preliminaries

1. ViT's standard structure

우선, input image는 N개의 flattne된 2D pathces로 분할되고 이는 embedding layer를 거쳐 D-dimensional vector로 projection됩니다. 이를 matrix로 $X_0 \in \mathbb{R}T^{N \times D}$와 같이 표시합니다. 

다음으로, $X_0$는 transformer blocks의 stack을 통과하게 됩니다. block은 Multi-head self-attention (MSA) module과 Multi-layer perceptron (MLP) module로 구성돼 있으며 각 moudle은 통과하기 이전에 Layer-Norm을 적용하고 residuals를 더해줍니다. 이를 수식으로 나타내면 아래와 같이 나타낼 수 있습니다.

$\textbf{Y}_{l-1} = MSA(LayerNorm(\textbf{X}_{l-1})) + \textbf{X}_{l-1}$

$\textbf{X}_l = MLP(LayerNorm(\textbf{Y}_{l-1})) + \textbf{Y}_{l-1}$

여기서 $l= 1, 2, ..., L$이고  $L$은 transformer block의 수입니다.

 

MSA(Multi-head Self Attention) module은 input을 $X' \in \mathbb{R}^{N \times D}$라할 때, patch간의 correlations를 학습시킵니다. 이를 수식으로 표현하면 아래와 같이 표현할 수 있습니다.

$[\textbf{Q}_i, \textbf{K}_i, \textbf{V}_i] = \textbf{X}'\textbf{W}^{qkv} + b^{qkv} \ i= 1,2, ..., h$

$Attn_i = Softmax(\frac{\textbf{Q}_i \ \textbf{K}^T_i}{\sqrt{D_h}})\textbf{V}_i$

$MSA(\textbf{X}') = [Attn_1, Attn_2, ... , Attn_h]\textbf{W}^o + b^o$

여기서 $W^{qkv} \in \mathbb{R}^{D \times 3D_h}, b^{qkv} \in \mathbb{R}^{3D_h}, W^o \in \mathbb{R}^{h D_h \times D}, b^o \in R^D$이고 $D_h$는 각 head의 feature size입니다.

 

MLP module은 MSA에서 얻은 feature들을 통해 representation을 학습하기 위해 $D_f$ dimension으로 projection 시킨 이후 이를 다시 $D$ dimension으로 projection 시킵니다.

$MLP(\textbf{Y}') = GELU(\textbf{Y}' \textbf{W}^1+ \textbf{b}^1)\textbf{W}^2 + \textbf{b}^2$

여기서 $\textbf{W}^1 \in \mathbb{R}^{D \times D_f}, \textbf{b}^1 \in \mathbb{R}^{D_f}, W^2 \in \mathbb{R}^{D_f \times D}, \textbf{b}^2 \in \mathbb{R}^D$입니다.

 

여기서 볼 수 있듯이 ViT는 많은 matrix multiplication이 필요하고 computational cost가 큽니다. 따라서 저자는 LayerNorm과 Softmax operation은 floating-points로 남겨두고 모든 weights와 matrix multiplication의 input을 quantization 합니다. 

2. Hardware-friendly quantizers

두 종류의 Hardware-friendly quantizer인 uniform quantizer와 log2 quantizer에 대해 설명하겠습니다.

 

uniform quantizer는 hardware-friendly한 가장 잘 알려진 quantizer 중 하나입니다. $x$와 $x^{(Z)}$를 각각 floating-point value와 quantized value, $\lfloor \rceil$를 round function, $b \in N$을 quantization bit-width라고 할 때 아래와 같이 표현할 수 있습니다.

$\text{Quant} : x^{(z)} = \text{clip} \left( \left\lfloor \frac{x}{s} \right\rfloor + z, 0, 2^b - 1 \right)$

$\text{DeQuant} : \hat{x} = s \left( x^{(z)} - z \right) \approx x$

$s \in \mathbb{R}^{+}$는 quantization scale이고 $z \in \mathbb{Z}$는 zero-point로서 아래와 같이 $x$의 lower, upper bound를 이용해 정의됩니다.

$s = \frac{\max(x) - \min(x)}{2^b - 1}, \quad z = \left\lfloor \frac{-\min(x)}{s} \right\rfloor$

 

log2 wuantizer는 또 다른 잘 알려진 hardware-oriented quantizer입니다. 여기서는 post-Softmax activations에만 사용되기 때문에(softmax activations의 결과는 양수이기 때문에) 아래와 같이 positive value quantization의 경우만 고려합니다.

$\text{Quant} : x^{(z)} = \text{clip} \left( \left\lfloor -\log_2 \frac{x}{s} \right\rfloor, 0, 2^b - 1 \right)$
$\text{DeQuant} : \hat{x} = s \cdot 2^{-x^{(z)}} \approx x$

log2에 이은 round function과 base-2 power function은 bit-shifting 연산을 이용해 빠르게 계산될 수 있으며 hard-ware friendly함을 알 수 있습니다. 

2. Methodology

이해를 돕기 위해 위의 Algorithm의 순서를 따라 설명하겠습니다.

 Pretrained full-precision model과 Calibration data를 가지고  post-Layernorm activations

Pretrained model은 Calibration data를 이용해 post-LayerNorm activations $\textbf{X}$'에는 channel-wise quantization$(s, z)$을 적용하고 post-Softmax activations $\textbf{A}$에는 $log \sqrt{2}$ quantizations$(s)$를 적용하여 초기화 됩니다. 

이후 이 초기화된 model은 Scale reparameterization을 통해 Inference시 효율성을 향상시키며 그 과정은 각각 아래와 같같습니다.

1. Scale Reparameterization for LayerNorm Activations

ViT에는 input $\textbf{X} \in \mathbb{R}^{N \times D}$의 normalization을 위해 아래와 같이 LayerNorm이 적용됩니다. 

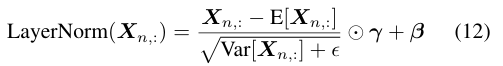
여기서 $n = 1,2, ..., N.$이며 $E[\textbf{X}_{n,:}$와 $Var[\textbf{X}_{n,:}]$은 각각 mean과 variance이고 $\gamma \in \mathbb{R}^D$와 $\beta \in \mathbb{R}^D$는 row vector입니다. $\odot$은 Hadamard product로서 element-wise multiplication이라고 보시면 됩니다.

 

post-LayernNorm activations의 결과를 살펴보면 아래와 같이 inter-channel variation이 큰 것을 볼 수 있습니다.

이 때문에, layer-wise quantization을 할 경우, 이러한 variation으로 인해 각 channel에 동일한 quantization scale을 적용하게 되면 상당한 accuracy degradation이 발생하게 됩니다. 따라서 channel-wise quantization을 이용하여야 accuracy degradation을 줄일 수 있습니다. 하지만 channel-wise quantization은 hardware의 support와 computational overhead가 있다는 단점이 있습니다.

 

저자는 scale reparameterization을 통해서 quantization과정과 inference과정을 분리함으로서, channel-wise quantization의 accuracy 와 layer-wise quantization의 efficiency를 모두 이용할 수 있도록 하였습니다.  그 과정을 지금부터 상세히 설명드리겠습니다. 우선, post-LayerNorm activations를 $\textbf{X}'$이라고 할 때, channel-wise quantization을 적용해 row vector quantization scale $\textbf{x} \in \mathbb{R}^D$와 zero-point $\textbf{z} \in \mathbb{Z}^D$를 구합니다. (quantization) 다음으로 Inference시 효율성을 위해 이를 다시, $\textbf{s} = \tilde{s} \cdot \textbf{1}$, $\textbf{z} = \tilde{z} \cdot \textbf{1}$과 같이 reparameterization 해줍니다. 여기서  $\textbf{1}$은 D-dimensioanl row vector로서 모두 1로 구성 돼 있습니다. $\tilde{s} \in \mathbb{R}^1$와 $\tilde{z} \in \mathbb{Z}^1$는 다음과 같이 정의 됩니다. $\tilde{s} = E[\textbf{s}]$, $\tilde{z} = E[\textbf{z}]$. variation factors 를 다음과 같이 정의하면 $\textbf{r}_1 = \textbf{s} / \tilde{\textbf{s}}$, $\textbf{r}_2 = \textbf{z} - \tilde{\textbf{z}}$ 이를 이용하여 $\beta$와 $\gamma$를 아래와 같이 $\tilde{\beta}$, $\tilde{\gamma}$로 reparameterization해주게 됩니다.

이렇게 하면 Inference시에 $\textbf{X}'$을$\tilde{s}$와 $\tilde{z}$를 이용해 quantization할 수 있고, $\tilde{\beta}$, $\tilde{\gamma}$로 새롭게 정의된 Affine factors를 이용하면 아래와 같이 distribution이 shift됩니다.

이를 보정해주기 위해 다음 layer's의 weigt와 bias를 아래와 같이 변경해줍니다.

이렇게 보정을 해주는 근거는 아래의 수식을 보면 이해하실 수 있습니다.

여기서 $j = 1, 2, ..., 3D_h$입니다.

그런데 이때, $\textbf{r}_1 \in \mathbb{R}^D$와 $\textbf{W}^{qkv}$의 quantization scale $\textbf{s}^{qkv} \in \mathbb{R}^{3D_h}$, zero-point $\textbf{z}^{qkb} \in \mathbb{R}^{3D_h}$가 차원이 맞지 않기 때문에 re-calibration을 해줘야 합니다. channel-wise로 quantization하기 때문에 $\textbf{r}_1$의 적용으로 performance에 큰 차이가 발생하지 않고, 근소한 accuracy의 감소만 발생시킵니다.

 

1. Scale Reparameterization for post-Softmax Activations

ViT에서 MSA module을 통해 계산된 attention scores를 probabilities 형태로 바꿔주기 위해 Softmax activations이 사용됩니다.  Sofmax activations를 사용한 결과인 post-Sofmtax activations의 분포를 살펴보면 아래에 첨부한 그림과 같이 균형잡힌 Gaussian 또는 Laplace distributions와 달리 상당히 unbalanced하고 power-law distributions와 같은 형태를 뛰는 것을 볼 수 있습니다. 작은 값들이 주를 이루지만 사실 정말 중요한 값들은 1에 가까운 큰 값들이기 때문에 이러한 값들이 clipped되면 성능에 큰 영향을 주게 됩니다.  

이러한 문제를 해결하기 위해 이전의 연구에서는 $log2$ quantizer를 사용합니다. uniform quantizer에 비해서 좋은 성능을 내긴 했지만 여전히 개선이 필요했고 저자는 $log \sqrt{2}$ quantizer를 이용해 이를 해결합니다. $log \sqrt{2}$ quantizer는 큰 values들에 대해 higher quantization resolution을 제공하고 distribution을 더 정확하게 묘사합니다. 하지만 그대로 사용할 경우, hardware-friendly한 $log2$ quantizer의 이점을 사용하지 못한다는 문제가 발생하고 저자는 이를 마찬가지로 reparameterization으로 quantization-inference decoupling을 하여 이 문제를 해결합니다.

 

post-Softmax activations를 $\textbf{A}$ $log\sqrt{2}$ quantizer의 scale을 $s \in \mathbb{R}$이라고 할 때, log의 base chaning formula를 이용하면 아래와 같이 $log\sqrt{2}$ quantizer를 $log_2$를 이용해 나타낼 수 있습니다. 

이를 통해 quantization procedure에서  $log\sqrt{2}$ quantizer는 단순히 2를 곱하여 log2 quantizer 형태로 변경할 수 있음을 알 수 있습니다.

유사하게 de-quantization procedure도 2's power의 bit-shifting operation의 이점을 이용하기 위해 아래와 같이 식을 변경할 수 있고 여기서 $\mathbf{1}(\cdot)$는 indicator function으로서  홀수이면 1이고 짝수이면 0이다.

indicator function과 coefficients는 모두 s와 함께 병합되어 아래의 식처럼 $\tilde{s}$로 reparameterization할 수 있고  결과적으로 de-quantization procedure는 bit-shifting operations를 이용하고 $\tilde{s}$의 indicator function이 계산 편리성을 이용할 수 있게 됩니다.

3. 주요 Experiment 결과

1. Quantization Results on ImageNet Dataset (Image Classification)

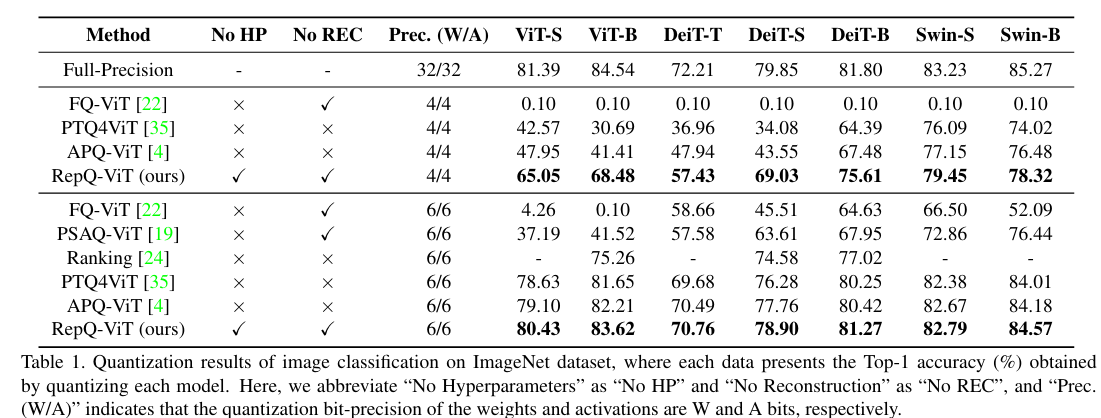
2. Quantization Results on COCO Dataset (Object detection and Image recognition)

 

3. Ablation Studies

post-layerNoarm activations의 scale reparameterization과 post-Softmax activations의 scale reparameterization이 다른 methods와 달리 좋은 성능과 Hardware-friendly를 동시에 함을 만족시키는 것을 확인할 수 있습니다.

4. Efficiency Analysis

소량의 Calbriation Data를 이용하고 적은 time comspution에도 불구하고 좋은 성능을 내는 것을 확인할 수 있습니다.

4. Conclusion 및 제안

이 논문에서 저자는 Scale reparameterization을 통해 quantization-inference를 decouple하여 Hardware-friendly하면서도 좋은 성능을 내는 ViT의 PTQ methods를 제안하였습니다.

 

앞선 PTQ 논문에서 distribution을 유지하는 것이 loss degeneration을 최소화하는 방향이 아님을 보였고 수학적으로도 증명하였습니다. 그렇기에 BRECQ와 같은 PTQ 방법을 scale reparameterization을 통해 hardware efficiency를 높이는 방법은 없을지 확인해보고 싶다는 생각을 하였습니다.