1. Introduction
Quantization 방법은 크게 PTQ(Post-Training Quantization)과 QAT(Quantization-Aware Training) 두 가지로 분류할 수 있다.
QAT(Quantization-Aware Training)는 original model을 training 한 이후, quantized 모델을 fine-tune 하는 방법이다. Full training dataset을 이용하고 end-to-end backpropagation을 사용하기 때문에 많은 computation resources를 요구하고, 이 때문에 compressed models를 만들 기 위해선 많은 시간이 소요된 다는 단점이 있다. 추가로, privacy 문제로 Full data set을 이용하지 못하는 경우엔 QAT를 사용하지 못한다는 문제가 있다.
PTQ(Post-Training Quantization)는 end-to-end retraining 없이, 또는 소량의 trainig data만을 이용하여 quantization을 하는 방법을 말한다. QAT와 비교하여 빠르게 quantized model을 얻을 수 있다는 장점이 있으나, 일반적으로 Accuracy가 QAT에 비해 좋지 못하다는 문제가 있다. 대부분의 PTQ는 parameter space에서 approximation을 하는데 이는 model space의 approximation과 차이가 있기에 final task loss의 optimal minimization을 보장하지 못하기 때문이다.

이러한 문제를 알아차린 이후부터, Nagel et al,, 2020 등에서는 quantization에 의한 loss degradation을 Taylor series expansion을 통해 근사하고 이를 minimize 하기 위해 노력하였다.
그러나 이것만으로는 INT2까지 weights를 quantization 할 수는 없었는데, 이 논문에서는 이를 wieght의 peturbation이 클 경우, taylor sereis의 second-order term인 Hessian matrix의 cross-layer dependency를 무시할 수 없기 때문이라고 보았다. 이 논문에서 저자는 second-order error를 Guass-Newton Matrix로 근사하고 generalization 성능을 향상하기 위해 block reconstruction이라는 방법을 사용한다. 저자가 제안하는 세 가지 contributions은 다음과 같다.
1. Second-order error의 분석을 통해 block reconstruction을 제안하였으며 FIM을 이용해 pre-activation Hessian의 계산을 간단히 하였다.
2. Genetic algorithm을 이용해 mixed precision 시, 적합한 layer precision의 조합을 찾아냈다. 또 latency and size guaranteed mixed precision 결과를 통해 specialized hardware FPGA와 general hardware ARM CPU에서도 좋은 성능을 냄을 확인하였다.
3. BRECQ는 다양한 models과 tasks에 적용이 가능하며 PTQ method 중 처음으로 2-bit weight quantization에 성공하였다.
2. Preliminaries
1. Notations
Vectors: small bold letter로 표시 ex) w: weight tensor의 flattened version
Matrices(or Tensors): capital bold letter로 표시 ex) W: weight tensor
Expectation over data points: Bar accent로 표시 ex) $\bar{\textbf{a}}$
Layer Index: bracketed superscript ex) $\textbf{w}^{(l)}$
Convolutional or fc layer's input and output vectors: input x, output z
Activation function: h() (이 논문에서는 ReLU를 사용)
n layers neural network의 forward pass는 아래와 같이 표현 가능하다.
$\textbf{x}^{(l+1)} = h(\textbf{z}^{(l)}) = h(\textbf{W}^{(l)}\textbf{x}^{(l)} + \textbf{b}^{(l)}), \quad 1 \leq l \leq n$
(bias $\textbf{b}^{(l)}$의 경우 생략 가능.)
Frobenius norm: $||*|||_F$
For $m \times n$ matrix $\textbf{A}$, Frobenius norm $||\textbf{A}|||_F$
1. = $|a_{11}|^2 + ... + |a_{mn}|^2 $
2. = $tr(A^TA)$
3. = $|\sigma_1|^2 + ... + |\sigma_r|^2 $
2. Quantization Background (Skip 가능)
편의를 위해 Uniform symmetric quantizatizer를 생각해 보자.
Unifrom symmetric quantizer는 floating point numbers를 several fixed-points로 mapping 시키며 이 points들은 같은 interval를 같고 대칭적으로 분포한다. 이 grids의 집합을 $Q^{u,sym}_b = s \times \{-2^{b-1}, ... , 0, ... , 2^{b-1} -1\}$와 같이 표현할 수 있고 여기서 $s$는 step size, $b$는 bit-width이다. Quantization function을 $q: R \rightarrow Q^{u,sym}_b $와 같이 표현할 때 아래와 같이 정의되는 quantization error를 최소화하는 quantizatizer는 rounding to nearest operation이다.
$ \min || \hat{\textbf{w}} - \textbf{w} ||^2_F. \quad s.t. \hat{\textbf{w}} \in Q^{u,sym}_b $
앞서 언급했듯이, parameter space에서 quantization error를 최소화하는 것은 quantized 된 network의 optimal task performance를 가져오지 않는다. 따라서 objective를 아래와 같이 수정할 수 있다.
$\min \ E[L(\hat{\textbf{w}})] \quad s.t. \hat{\textbf{w}} \in Q^{u,sym}_b $
QAT의 경우 이 objective는 비교적 쉽게 달성할 수 있으나, PTQ에서는 $\textbf{w}^* = arg \min_\textbf{w} E[L(\textbf{w})]$ where $\textbf{w} \in R$ 과 training data의 일부만 접근 가능하기 때문에 QAT에 비해 상대적으로 어려움이 있다.
3.Taylor Expansion
Quantization 된 weights를 weight perturbation처럼 생각할 수 있고 Nagel et al. (2020)에서는 Taylor series expansions를 이용해 quantization에 의한 loss degradation을 다음과 같이 근사한다.
$E[L(\textbf{w} + \Delta \textbf{w})] - E[L(\textbf{w})] \approx \Delta \textbf{w}^T \bar{\textbf{g}}(\textbf{w}) + \frac{1}{2} \Delta \textbf{w}^T \bar{\textbf{H}}(\textbf{w}) \Delta \textbf{w}$
여기서 $ \bar{\textbf{g}}^{(\textbf{w})} = E[\nabla_{\textbf{w}} L]$이고 $ \bar{\textbf{H}}^{(\textbf{w})} = E[\nabla^2_{\textbf{w}} L]$이다. 또 $\Delta \textbf{w}$는 weight perturbation이다.
pre-trained model이 minimum으로 converge하기 때문에 FONC에 의해 $ \bar{\textbf{g}}^{(\textbf{w})}$는 $\textbf{0}$이라 생각할 수 있고 아래와 같이 second-order approximation형태로 나타낼 수 있다.
$E[L(\textbf{w} + \Delta \textbf{w})] - E[L(\textbf{w})] \approx \frac{1}{2} \Delta \textbf{w}^T \bar{\textbf{H}}(\textbf{w}) \Delta \textbf{w}$
여기서 한 가지 문제점이 발생하는데, full Hessian은 많은 device에서 memory infeasiable 하다는 것이다. (terabytes of memory space를 필요로 한다.)
Nagel et al. (2020)에서는 이를 아래의 두 가지 가정을 이용해 해결 한다.
1. Layers가 mutal-independet 하다는 것이다. 따라서 Hessian을 layer-diagonal 형태로 표현하고 $\bar{\textbf{H}}^{(\textbf{w}^{(l)})} \approx E[\textbf{x}^{(l)}\textbf{x}^{(l),T} \otimes \textbf{H}^{(\textbf{z}^{(l)})} ]$과 같이 근사한다. 여기서 $\otimes$ 는 Kronecker product이다.
2. pre-activations의 Hessian은 Input data와 무관하게 constant diagonal matrix로 근사한다. ($ \textbf{H}^{(\textbf{z}^{(l)})} = c \times \textbf{I}$)
다양한 study에서 이러한 layer-wise objective를 사용하였으나 모두 INT2까지 weights를 quantize 하는데 실패하였다. 저자는 이를 $\Delta \textbf{w}$가 커질수록, 위의 가정이 성립하지 않기 때문이라고 봤고 더 정확한 근사가 필요하다고 보았다.
3. Methods
1. Cross-Layer Dependency
neural network의 output을 $\textbf{z}^{(n)} = f(\theta)$라고 할 때, loss function은$L(f(\theta))$와 같이 표현할 수 있다. 여기서 $\theta$는 $vec[\textbf{w}^{(1),T}, ... , \textbf{w}^{(n),T}]^T$로서 모든 n layers의 weights vector의 stack이다.
Hessian matrix의 (i,j) element는 chain rule에 의해 아래와 같이 표현할 수 있다.
$\frac{\partial ^2 L}{\partial \theta_j \partial \theta_i} = \frac{\partial}{\partial \theta_j} (\sum_{k=1}^m \frac{\partial L}{\partial \textbf{z}^{(n)}_k} \frac{\partial \textbf{z}^{(n)}_k}{\partial \theta_i}) = \sum_{k=1}^m \frac{\partial L}{\partial \textbf{z}^{(n)}_k} \frac{\partial^2 \textbf{z}^{(n)}_k}{ \partial \theta_j \partial \theta_i} + \sum_{k, l=1}^m \frac{\partial \textbf{z}^{(n)}_k}{\partial \theta_i} \frac{\partial^2 L}{ \partial \textbf{z}^{(n)}_l \textbf{z}^{(n)}_k} \frac{\partial \textbf{z}^{(n)}_l }{\partial \theta_j} \quad where \quad \textbf{z}^{(n)} \in R^m$
여기서 $\sum_{k=1}^m \frac{\partial L}{\partial \textbf{z}^{(n)}_k} \frac{\partial^2 \textbf{z}^{(n)}_k}{ \partial \theta_j \partial \theta_i}$는 pretraiend full precision model이 local minimum으로 converge한다고 가정하면 FONC에 의해 $\nabla_{\textbf{z}^{(n)}}L \approx \textbf{0}$이기 때문에 생략이 가능하다. 결과적으로, $\frac{\partial ^2 L}{\partial \theta_j \partial \theta_i} = \frac{\partial}{\partial \theta_j} (\sum_{k=1}^m \frac{\partial L}{\partial \textbf{z}^{(n)}_k} \frac{\partial \textbf{z}^{(n)}_k}{\partial \theta_i}) \approx \sum_{k, l=1}^m \frac{\partial \textbf{z}^{(n)}_k}{\partial \theta_i} \frac{\partial^2 L}{ \partial \textbf{z}^{(n)}_l \textbf{z}^{(n)}_k} \frac{\partial \textbf{z}^{(n)}_l }{\partial \theta_j} \quad where \quad \textbf{z}^{(n)} \in R^m$ 와 같이 근사가 가능하다.
이를 matrix 형태로 표현하면 $\textbf{H}^{\theta} \approx \textbf{G}^{\theta} = \textbf{J}_{\textbf{z}^{(n)}}(\theta)^T \textbf{H}^{(\textbf{z}^{(n)})} \textbf{J}_{\textbf{z}^{(n)}}(\theta) $와 같이 표현할 수 있고 이 $\textbf{G}^{\theta}$를 Gauss-Newton (GN) matrix라고 한다. (여기서 $\textbf{J}_{\textbf{z}^{(n)}}(\theta)$는 network parameter $\theta$에 대한 network output $\textbf{z}^{(n)}$의 Jacobian matrix이다.)
$\textbf{H}^{\theta}$를 위와 같이 Gauss-Newton Matrix로 근사하려해도 Jacobain matrix를 explicit 하게 compute 하고 저장하는데 현실적으로 무리가 있다. 이를 저자는 아래의 Theorem을 이용해 해결을 한다.

간단히 설명하면, 앞서 설명했던 second-order weight perturbation error $E[L(\theta + \Delta \theta)] - E[L(\theta)] \approx \frac{1}{2} \Delta \theta^T \bar{\textbf{H}}^{(\theta)} \Delta \theta$ 를 Gauss-Netwon Matrix를 이용해 $E[L(\theta + \Delta \theta)] - E[L(\theta)] \approx E[ \frac{1}{2} \Delta \theta^T \textbf{J}_{\textbf{z}^{(n)}}(\theta)^T \textbf{H}^{(\textbf{z}^{(n)})} \textbf{J}_{\textbf{z}^{(n)}}(\theta) \Delta \theta ]$ 와 같이 근사할 수 있고,
$\Delta \textbf{z}^{(n)} \approx \textbf{J}_{\textbf{z}^{(n)}}(\theta) \Delta \theta$ 를 이용해 한 번 더 근사하여 $\frac{1}{2} E[L(\theta + \Delta \theta)] - E[L(\theta)] \approx E[ \Delta \textbf{z}^{(n),T} \textbf{H}^{(\textbf{z}^{(n)})} \Delta \textbf{z}^{(n)} ]$로 표현하겠다는 것이다. 결과적으로, large-scale second-order error를 output Hessian $ \textbf{H}^{(\textbf{z}^{(n)})}$과 $\Delta \textbf{z}^{(n)}$으로 표현할 수 있고 network의 final output $ \textbf{z}^{(n)}$의 reconstruction을 통해 quantization으로 인한 discrepency를 최소화 할 수 있다는 말이다. 다른 말로, Quantization의 목적을 network distillation이라고 볼 수도 있다는 말이다. 하지만 Network distillation은 일반적으로 normal training과 동일한 computation과 data resouce를 요구하기에 PTQ에는 부적합하다고 볼 수 있다.
2. Block Reconstruction
앞장에서 설명한 network output reconstruction은 second-order error를 PTQ layer-by-layer reconstruction에 비해 정확하게 estimate 한다는 장점이 있으나, layer-by-layer에 비해 실제론 좋은 결과를 가져오지 못하였다. 그 원인을 저자는 PTQ의 적은 training data로 인해 network가 쉽게 over-fitting 되기 때문이라고 보았다. 또 layer-wise reconstruction에서 각 layer를 독립적으로 output distribution을 matching하는 것은 일종의 regularization 처럼 동작하여 generalization error를 감소시킨다고 보았다.
여기에서 아이디어를 얻어 저자는 더 좋은 bias-variance trade-off의 선택을 위해 적절한 granularity를 선택하면 어떨까? 라는 생각을 한다.

Layer diagonal optimization은 위의 그림 Figure 1(b)에서 파란색 Layer diagonal Hessian으로 표현 가능하고, Network-wise optimization은 Figure 1(b)의 초록색 Full Hessian에 해당한다.
중간 granularity의 block-diagonal Hessian의 경우,
layer k에서 부터 layer l이 block을 형성할 때 ($1 \leq k \leq l \leq n$) 이 block에 해당하는 weight vector는 $\tilde{\theta} = vec[\textbf{w}^{(k),T}, ... , \textbf{w}^{(l),T}]^T$와 같이 표현할 수 있다.
discrepency는 $\Delta \tilde{\theta}^T \bar{\textbf{H}}^{(\tilde{\theta})} \Delta \tilde{\theta} = E[ \Delta \textbf{z}^{(l),T} \textbf{H}^{(\textbf{z}^{(l)})} \Delta \textbf{z}^{(l)} ]$ 로 나타낼 수 있다.
이처럼 block-diagonal Hessian은 inter-block dependency를 무시하고 intra-block dependancy만을 고려하여 block-by-block으로 intermediate output을 reconstruct한다.
이처럼 저자는 2개의 intermediate reconstruction granularity(Stage-wise reconstruction, Block-wise reconstruction)를 정의하여 아래와 같이 총 4개의 reconstruction granularity에 대해서 실험을 진행한다.

실험 결과, 저자는 Block-wise Reconstruction이 다른 것들에 비해 좋은 성능을 내는 것을 발견하였고 이는 Hessian의 main off-diagonal loss가 각 block 단위로 집중돼 있기 때문이라고 보았다. inter-block loss는 상대작아서 optimization에서 무시 가능하다고 보았으며 stage-wise나 net-wise optimization의 경우, generalization 능력이 좋지 않아 final performance를 감소 시킨다고 보았다. 저자는 이렇게 Block-wise로 reconstruction하는 것을 BRECQ라는 이름을 붙였다. Block-wise로 optimization 하는 것은 실험으로 부터 내린 결론이며 아래 두 가지 장점을 갖는다.
1. Hyper parameters가 필요 없다.
2. 모든 models과 모든 tasks에 적용이 가능하다.
3. Approximating Pre-Activation Hessian
Block-wise Reconstruction을 위해선, $E[ \Delta \textbf{z}^{(l),T} \textbf{H}^{(\textbf{z}^{(l)})} \Delta \textbf{z}^{(l)} ]$을 통해 block의 second-order error를 계산해야 한다. 이 때 pre-activation Hessian $\textbf{H}^{(\textbf{z}^{(l)})}$의 계산이 문제가 되는데, 이 논문에서는 diagonal Fisher Information Matrix (FIM)을 이용해 pre-activation Hessian을 근사하여 이를 해결한다. FIM에 관해서는 이 링크의 블로그 설명을 보면 쉽게 이해할 수 있다.
$\theta$를 parameter로 가지는 $x$의 확률 분포를 $p_{\theta}(x)$ 또는 $p(x|\theta)$와 같이 나타낼 수 있고 FIM은 negative log likelihood의 expected Hessian과 같고 loss L이 cross entropy loss이기 때문에 $\textbf{H}^{(\theta)}_L = E[ \nabla_{\theta} L \ \nabla_{\theta} L^T ]$과 같이 표현할 수 있음을 알 수 있다. 이를 수식으로 나타내면 아래와 같다.
$ \textbf{H}^{(\theta)}_L = E[-\nabla_{\theta}^2 \log p_{\theta}(x)] = -E[\nabla_{\theta}^2 \log p_{\theta}(x)] = E[\nabla_{\theta} \log p_{\theta}(x) \nabla_{\theta} \log p_{\theta}(x)^T ] = E[ \nabla_{\theta} L \ \nabla_{\theta} L^T ] = FIM(\theta)$
pre-activation FIM의 diagonal을 이용해 pre-activation Hessian $\textbf{H}^{(\textbf{z}^{(l)})}$을 근사하면 아래와 같이 Block-wise reconstruction을 할 수 있다.
$\min_{\hat{\mathbf{w}}} \mathbb{E} \left[ \Delta \mathbf{z}^{(\ell)\top} \mathbf{H} (\mathbf{z}^{(\ell)}) \Delta \mathbf{z}^{(\ell)} \right] = \min_{\hat{\mathbf{w}}} \mathbb{E} \left[ \Delta \mathbf{z}^{(\ell)\top} \operatorname{diag} \left( \left( \frac{\partial L}{\partial \mathbf{z}_1^{(\ell)}} \right)^2, \ldots, \left( \frac{\partial L}{\partial \mathbf{z}_a^{(\ell)}} \right)^2 \right) \Delta \mathbf{z}^{(\ell)} \right].$
위의 equantion에서 볼 수 있듯이, BRECQ는 어떠한 optimization method에도 적용이 가능하며 저자는 weights에는 adaptive rounding, activation에는 learned step size를 사용하였다.
calibration algorithm을 정리하여 나타내면 아래와 같다.




저자는 quantization을 위해 전체 dataset의 일부만을 사용하였으며, single GTX 1080T1 GPU를 이용해 20분 만에 quantized된 ResNet-18을 얻을 수 있었다.
4. Mixed Precision
저자는 PTQ의 성능 향상을 위해 모든 layer의 precision을 통일하는 대신, mixed precision techniques를 사용하고 이는 아래와 같이 표현가능하다.
$\min_{\mathbf{c}} L(\hat{\mathbf{w}}, \mathbf{c}), \quad \text{s.t.} \ H(\mathbf{c}) \leq \delta, \quad \mathbf{c} \in \{2, 4, 8\}^n.$
여기서 $\textbf{c}$는 number of layers n shape의 bit-width vector이다. H(*)는 hardware performance measurement function으로서 사전에 정의한 threshold $\delta$ 이하가 되도록 한다. mixed precision 선택에 있어서 2, 4, 8 bit를 사용하는데 일반적으로 이 bit들이 많이 사용되기 때문이다.
최적의 bit 조합의 선택을 위해 저자는 Genetic algorithm을 이용하는데, Genetic Algorithm은 간단히 설명하면, 자연 선택 및 유전 메커니즘을 모방한 최적화 알고리즘이라고 할 수 있다. 자세한 설명은 이 링크의 설명을 참여하길 바란다.

4. Expreimetns
1. Ablation Study
4종류의 reconstruction granularity를 test하였다. ImageNet dataset을 사용했으며, MobileNetV2, ResNet-18을 Architecture로 사용하였다. 첫 번째와 마지막 layer를 제외한 모든 layers를 2-bit quantization한 결과는 아래와 같다.
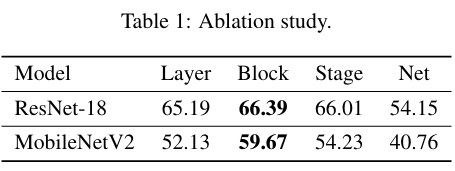
실험결과, Block-wise reconstruction이 다른 granularity에 비해 좋은 성능을 내는 것을 확인하였고, generalization error의 증가에 있어 off-diagonal loss가 영향을 미치고 Block-wise reconstruction이 generalization error를 최소화 한다는 결론을 내렸다.
2. IMAGENET
다양한 network architecture에 대해 BRECQ를 비롯해 여러 quantization method의 성능을 비교한 결과이다.

다른 methods에 비해 PTQ quantization임에도 불구하고 performance degradation이 현저히 낮았고 좋은 성능을 보였다. 또 처음으로 2-bit weight, 4-bit activation PTQ quantization을 성공하였다.
3. COMPARISON WITH QAT

위의 Table은 QAT methods와 PTQ methods의 accuracy, Training cost 등을 비교한 Table로 BRECQ는 다른 PTQ methods와 달리 QAT methods와 comparable한 accuracy를 갖고, Traning cost 즉, GPU hours는 훨씬 적게 소요되는 것을 확인할 수 있었다.
MobieNetV2의 경우 심지어 PTQ methods의 성능을 띄어넘기까지 한다.
4.MS COCO
Object Detection에도 마찬가지로 적은 performance degradation을 보이며 좋은 성능을 보였다.

5. MIXED PRECISION

저자는 (1) model-size guaranteed mixed precision과 (2) FPGA latency guaranteed mixed precision 두 가지 경우에 대해 mixed precision과 unified precision의 성능 차이를 비교하였다. ResNet-18, Mobile Net-V2, RegNetX-600MF architecture를 이용해 실험을 진행하였고, activation은 8-bit로 고정하였다. 위의 결과에서 볼 수 있듯이, Mixed Precision이 대체로 unified precision에 비해 좋은 성능을 보였으며, 특히 bit 수가 적이질수록 이러한 경향은 더 커졌다. 결과적으로 BRECQ는 여러 hardware 제약 조건 속에서도 좋은 성능을 유지함을 알 수 있었다.
5.Conclusion
Second-order error를 분석하여 제안한 PTQ framework인 BRECQ는 적절한 cross-layer dependency의 balance를 통해 다른 PTQ에 비해 눈에 띄는 성능 향상을 가져왔으며 처음으로 2-BIT PTQ weight quantization에 성공하였다. Mixed precision을 사용하여 조금 더 성능 향상을 이끌어낼 수 있었으며, QAT와 견줄만한 성능을 이끌어내는데 성공하였다.
'Quantization' 카테고리의 다른 글
| [논문 리뷰] RepQ-ViT: Reparameterization for Post-Training Quantization of Vision Transformers (1) | 2024.07.29 |
|---|
